Sample Size Calculator: Two Parallel-Sample Means

Note:

Help Aids Top

Application: This procedure is used to test whether there is a difference between the mean responses of the test drug and the placebo control or active control. The following hypotheses are usually considered:

Procedure:

1. Enter

a)      value of α, the probability of type I error

b)      value of β, the probability of type II error

c)      value of allowable difference

d)     value of Population variance

2. Click the button “Calculate” to obtain result sample size of each group n.

Formula:                                                      (*)

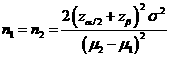Notations:

α:               The probability of type I error (significance level) is the probability of rejecting the true null hypothesis.

β:               The probability of type II error (1 – power of the test) is the probability of failing to reject the false null hypothesis.

μ₂ – μ₁:      The value of allowable difference is the true mean difference between a test drugs (μ₂) and a placebo control or active control agent (μ₁).

Examples

Example 1: Suppose a low density lipidproteins (LDLs) is considered of clinically meaningful difference. By using (*), assuming that the standard deviation is 10% (i.e., population variance is 0.01), the required sample size of each group to achieve an 80% power (β=0.2) at α=0.05 for correctly detecting such difference of μ₂ – μ₁=0.05 change obtained by normal approximation as n=63.

Example 2: It is desired to run a placebo-controlled parallel group trial in asthma. The target variable is forced expiratory volume in one second (FEV1). The clinically relevant difference is presumed to be 200 ml and the power should be 0.8. What should the sample size be?