Help Aids Top
Application: The determination of the number of patients needed in a prospective comparison of survival curves, when the control group patients have already been followed for some period, following hypotheses are usually used:
Procedure:
- Enter
a) value of α, the probability of type I error
b) value of δ, the minimum hazards ratio, it is specified in alternate hypothesis
(i.e. 
)
c) value of MS, the control median survival (month), it is estimated
from existing control data
d) value of r, the accrual rate (per
month), it is estimated for future accrual
e) value of nC,
the number
of deaths observed in the control, it is obtained from existing control data
f) value of yC, the number of patients
still at risk in the control, it is obtained from existing control data
g) value of τ, the
length of the planned continuation period (month)
h) value
of T, the length of the actual period for the new study (month).
- Click the button “Calculate” to obtain the power of the test and the sample size of patients in the experimental arm.
- Adjust the variable T (accrual time) until desire power is obtained (e.g. 80%).
Assumption:
1.
Time
to survival is exponential distributed with hazard rate λ.
2.
Prospective
studies are used.
3.
There
is no withdrawal or losses to follow-up.
Formula:
Null
hypothesis for two exponential distributions has a rejection region.
(1),
where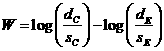 
,
number of failures observed in group
i,
total patient years of observation
time in group i,
is the upper
percentile of the standard normal distribution.
For
, where
is the true failure rate in group i, (1) is the critical region of
size
for the one-sided alternative
.
The
power of the test for a specific value of
is approximately
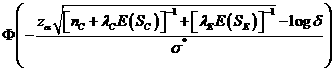(2),
where 
is the cumulative standard normal distribution function,
(3),
(4),
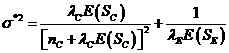(5),
nC is
the number of failures observed in the control group,
Si is the total additional observation time
to be observed in group i,
yC is the number still at risk in the
control group,
r is the accrual rate,
T
is the length of the accrual period for the new study,
is the length of the planned
continuation period.
Note: (If withdrawals are expected to occur at
rate
, then
and
in equation (3) and (4) should be replaced by
and
, respectively.) To calculate the power of a particular study,
one replacesby
and placesby
, where
is the total observation time already observed in the control
group. If additional follow-up of remaining controls were not possible, one
would set
to zero in (2).
Notations:
α: The
probability of type I error (significance level) is the probability of rejecting the true null
hypothesis.
β: The
probability of type II error (1 – power of the test) is the probability of
not rejecting the false null hypothesis.
Example:
Suppose one wishes to design a trial to compare new treatment E with control treatment C, on the basis of survival duration. Historical data for C from a recently compared trial are available: a total 100 patients, of whom 50 have already died (nC=50, yC=100-50=50), with a median survival of 12 months (MS=12). The aim is to have 80% power (P=80%) to detect a ratio of hazard rates of 1.5 (δ=1.5), using a one-sided, 5% significance level test (α =0.05) after a one-year continuation period (τ=12). Recent experience indicates that new eligible patients will arrive at the rate of three per month (r=3). The required accrual target is approximate 88 patients (N=88) with actual time about 29.3 months for the new study (T=29.3).
Reference: Dixon & Simon (1988) J Clin Epidemiol 41:1209-1213