Help Aids Top
Application:
Consider a 2×2 cross-over design contains two
sequences (treatment orderings) and two time periods (occasions). One sequence
receives treatment A followed by treatment B. The other sequence receives B and
then A. This procedure is used to test the following hypotheses: ![]()
Procedure:
- Enter
a) value of α, the probability of type I error
b) value of β, the probability of type II error
c)
value of allowable difference
d) value of population variance
- Click the button “Calculate” to obtain result sample size of each group n.
Formula:
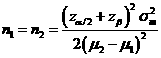 (*)
(*)
Notations:
α: The
probability of type I error (significance level) is the probability of rejecting the true null
hypothesis.
β: The
probability of type II error (1 – power of the test) is the probability of
failing to reject the false null hypothesis.
μ2 – μ1: The value of allowable difference is the true mean difference between a test drugs (μ2) and a placebo control or active control agent (μ1).
Examples
Example 1:
Suppose a low density lipidproteins
(LDLs) is considered of clinically meaningful
difference. By using (*), assuming that the standard deviation is 10% (i.e.,
population variance is 0.01), the required sample size of each group to achieve
an 80% power (β=0.2) at α=0.05 for correctly detecting such
difference of μ2 – μ1=0.5 change obtained by normal
approximation as n=16.
Reference: Chow, Shao and Wang, Sample Size Calculations In Clinical
Research,