Sample Size Calculator: One Sample Mean

Hypothesis: Two-Sided Equality

Data Input: (Help) (Examples)

Input

 

Results

α

 

 

 

β

N

Allowable difference

 

 

 

Population Variance

 

 

 

 

Note:

Variables

Descriptions

α

Two-sided significance level

1-β

Power of the test

Allowable difference

Acceptable difference between sample mean and known or expected population mean (μ - μ0)

Population Variance

Population variance

N

Sample size

Help Aids Top

 

Application: This procedure is used to test if there is a statistically significant difference between the mean response of an experimental drug and a constant reference value. The following hypotheses are usually considered:

 

Procedure:

  1. Enter

a)      value of α, the probability of type I error

b)      value of β, the probability of type II error

c)      value of allowable difference

d)     value of expected variance, the population variance.

  1. Click the button Calculate to obtain result sample size N.

 

Formula:                                                (*)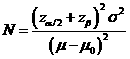

 

 

Notations:

 

α:             The probability of type I error (significance level) is the probability of rejecting the true null hypothesis.

 

β:             The probability of type II error (1 - power of the test) is the probability of failing to reject the false null hypothesis.

 

μ - μ0:      The value of allowable difference is the difference value between true mean and reference mean (constant value).

 

Examples

 

Example 1: A pharmaceutical company is interested in investigating the effect of a test drug on prevention of a progression to osteoporosis in women with osteopenia. We want to show that after treatment, the change in bone density from mean values is less than 1 unit (δ=1) assuming that the known mean bone density before the treatment is 1.5 (μ0=1.5). Now suppose that the mean bone density after treatment is expected to be 2. Thus we have μ - μ0=0.5, at α=0.05 with given variance of 1, the required sample size for having an 80% power (β=1-80%=0.2) for correctly detecting a difference of 0.5 change from pre-treatment to post-treatment can be obtained by normal approximation as N=32.

 

 

Reference: Chow, Shao and Wang, Sample Size Calculations In Clinical Research, Taylor & Francis, NY. (2003) Pages 48-50.

 

Top