C.I. Calculator: Two Sample Proportions

Data Input: (Help) (Example)

Input	Result
1-α	d
p1	Lower
p2	Upper
n1
n2

Note:

Variables	Descriptions
1-α	Two-sided confidence level
p1	Success proportion in sample 1
p2	Success proportion in sample 2
n1	Sample size of sample 1
n2	Sample size of sample 2
d	Difference between p2 and p1
Lower	Lower C.I.
Upper	Upper C.I.

---

Help Aids Top

Application:

It is to estimate the difference of 2 proportions and provide a confidence interval for the estimation.

Confidence intervals of difference not containing 0 imply that there is a statistically significant difference between the population proportions.

Procedure:

1. Enter

a)    Value of 1-α, the two-sided confidence level

b)    Value of p₁,p₂ the success proportion of each sample

c)    Value of n₁,n₂ the sample size of each sample

2. Click the button “Calculate” to obtain

a)    The difference between proportions of sample 2 and 1

b)    The 100(1-α)% confidence interval

3. Click the button “Reset” for another new calculation

Formula:

Define:

Define:

The 100(1-α)% confidence interval with continuity correction is defined as:

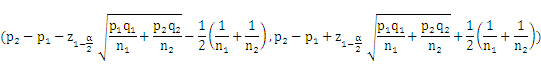
Notation:

100(1-α)% confidence interval: We are 100(1-α)% confident that the true value of the parameter is included in the confidence interval

: The z-value for standard normal distribution with left-tail probability

---

Example

Suppose there are two anti-microbial agents. The response rate of agent 1 is 0.244 (p₁=0.244), the response rate of agent 2 is 0.046 (p₂=0.046).

The sample size 1 is 197 (n₁=197) and the sample size 2 is 65 (n₂=65), the corresponding 95% C.I. ((1-α) = 0.95) is (-0.286911, 0.109089).

Top