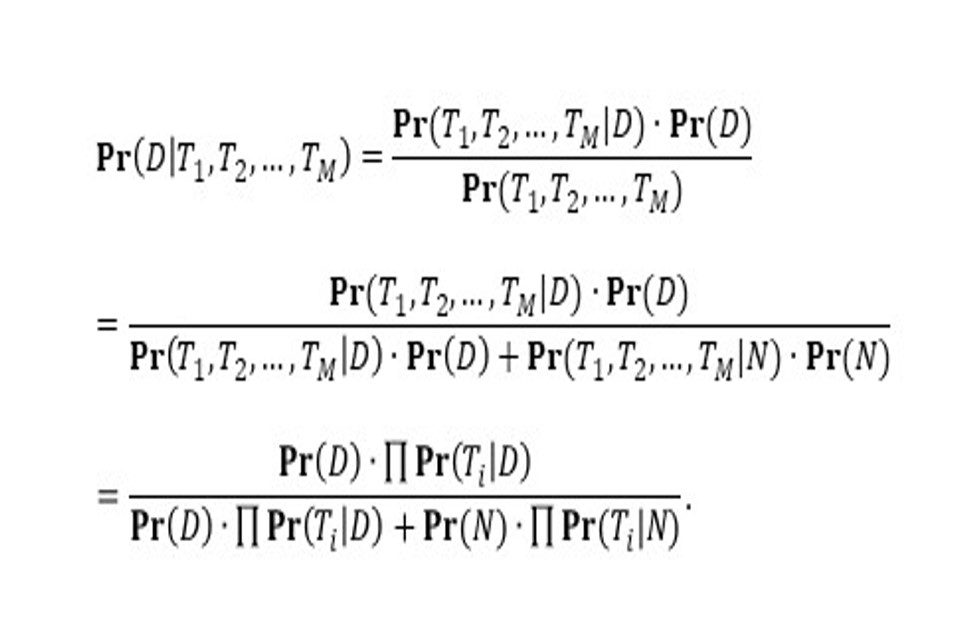This Diagnostic Assessment Tool is designed to assess the probability of subjects being infected by SARS-CoV-2 based upon multiple diagnostic testing outcomes and the pre-test probability of being infected.
Calculator: http://39.99.171.158:8080/COVID-19/
Procedure:
- Select up to 3 parallel or serial tests. Example scenarios:
- Scenario 1: Test #1: PR-PCR; Test #2: PR-PCR; Test #3: antibody test
- Scenario 2: Test #1: PR-PCR; Test #2: antibody test; Test #3: null
- Scenario 3: Test #1: chest CT; Test #2: null; Test #3: null
2. Input:
- “Sensitivity”, “Specificity” and “Outcome” for each test; and
- “Pre-test probability”: prevalence in the population if no contact history or symptom
3. Output:
- The “Results” will present the posterior probability of the subject being infected by SARS-CoV-2.
Theoretical Formulation:
We consider that one individual subject receives M diagnostic tests of COVID-19, where M is an integer and M > 1. The testing outcome, i.e., positive or negative, is denoted by Ti for the i-th test. We define Ti as a binary outcome that is 1 for positive testing outcome and 0 otherwise. We denote the event that ‘the individual subject has COVID-19’ by D (stands for ‘diagnosed’). For convenience, we also denote the complement of event D, i.e., ‘the individual subject does not have COVID-19’, by N (stands for ‘not diagnosed’). Straightforwardly, the summation of the probabilities (Pr) of D and N is 1. The posterior probability of D on the conditions of the M testing outcomes is Pr(D|T1, T2, …, TM). Hence, by using the Bayes theorem, the Pr(D|T1, T2, …, TM) can be computed by using Equation 1.
Here, Pr(Ti = 1|D) is the sensitivity of the i-th test, and Pr(Ti = 0|D) is its (1 – sensitivity). The Pr(Ti = 0|N) is the specificity of the i-th test, and Pr(Ti = 1|N) is its (1 – specificity). The Pr(D) indicates the pre-test probability of having COVID-19 for an individual who receives tests. An alternative interpretation of Pr(D) is the prevalence of the COVID-19 among the testing subjects. Hence, Pr(D|T1, T2, …, TM) is computable.
A Demonstrative Example:
Suppose one wishes to estimate the posterior probability under a two-test scenario. Two tests might be RT-PCR and chest CT. The sensitivity and specificity for RT-PCR and chest CT are available from previous studies or clinicians experience. We suppose 75% sensitivity and 95% specificity for RT-PCR, and 94% sensitivity and 37% specificity for chest CT and RT-PCR has a positive outcome and chest CT has a negative outcome, and the pre-test probability is 50%. Then, the posterior probability of the subject being infected with COVID-19 is 0.709.