Help Aids Top
Application: The
determination of the number of patients needed in a prospective comparison of
survival curves with losses to follow-up, when the control group patients have
already been followed for some period, following hypotheses are usually used: 
where 
is the hazard rate of patients in control group
is the hazard rate of patients in experimental group
Procedure:
- Enter
a) value of α, the probability of type I error
b) value of β, the probability of type II error, or (1-power) of the test
c) value of δ, the minimum hazards ratio, it is specified in alternate hypothesis
d) value of MS, the control median survival (month), it is estimated
from existing control data
e) value of QC, the proportion of patient in control group compared with
experimental group
f) value of QE, the proportion of patient in experimental group compared
with control group, where QC + QE = 1
h) value of T0, accrual duration (month), the length of time to recruit patients for
study
g) value of T-T0, follow-up duration (month, the length of study time of all recruited patients to the end of study T
- Click the button “Calculate” to obtain
a) value of N, the total sample size of patients in the control and experimental arm
b) value
of NC,
the sample size of patients in the control arm
c) value
of NE, the sample size of
patients in the experimental arm
d) value of D, the total
number of deaths at the end of study
Assumption:
1.
During
the accrual period of T years, patients enter trial according to a Poisson
process with rate n per year. They are randomized with equal probability to
either the control or experimental treatment.
2.
The
times from entry to death are independent with common exponential distribution
within each treatment. The median time to death for the control treatment is MC
and from a standard result for the exponential distribution, the death hazard
rate is
.
3.
The
times from entry to loss to follow-up are independent of each other and of the
entry times and death times. They have exponential distributions with
exponential loss to follow-up rates
for the control
group and
for the experimental group.
Theory:
We wish
to teat
at significance
level α and to have power 1-β against the alternative
for prespecified
.
Let
,
and
where
and
are observed numbers of deaths and
and
are observed total time at risk (person-years exposure) for
the control and treatment groups respectively.
Distribution
of 
is used because it is less skewed and have a more accurate
asymptotic approximation.
is asymptotically normally
distributed with mean
and variance
, where E donotes expectation.
Under
, the asymptotic size α test of 
rejects for 
, where 
and
is the standard normal (1- p) quantile.
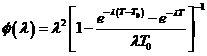
The
sample size to achieve specified significance level and power is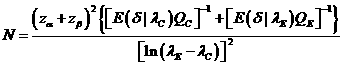
, where
is the upper 100(1-p) percentile
of the standard normal distribution.
The above equation can be changed to two-sided tests by changing the above α to α/2. Here the calculator we use two-sided test.
Notations:
α: The
probability of type I error (significance level) is the probability of rejecting the true null
hypothesis.
β: The
probability of type II error (1 – power of the test) is the probability of
not rejecting the false null hypothesis.
Example:
Consider that a clinical trial is to be conducted for a disease with moderate levels of mortality with hazard rare λ=1.22, yielding 50% survivors after 0.57 month (MS=0.57). Suppose that with treatment we are interested in a reduction in hazard rate (δ=1.3). With equal-sized group (QC=QE=0.5), a two sided significance level test (α =0.05) with power 80% power (β=0.2), and assume that recruitment was to be terminated after 4 years of a 5-year study (T=5, T0=4, T-T0=1), then the required sample size is approximate 498 (N=498) and the total number of deaths is 264 (ND=458).
Reference:
- Rubinstein, Gail, Santner (1981) J Chron Dis 8: 67-74
- Rubinstein, Gail, Santner (1981) J Chron Dis 34: 469-479