Help Aids Top
Application: Commonly, the central objective of Phase II clinical trials is the assessment of the antitumor ‘therapeutic efficacy’ of a specific treatment regimen. It is of interest to formulate test procedures which can be employed in these trials to decide whether or not this therapeutic efficacy warrants further investigation. One-sample multiple testing procedure is proposed which employs the standard single-stage test procedure at the last test.
Procedure:
- Enter
a) value of α, the probability of type I error
b) value of β, the probability of type II error, or (1-power) of the test
c) value of p0, the largest response probability
d) value of pA, the smallest response probability
e) value of Nmax, the maximum number of patients to be recruited
f) value of Numstage, the number of stages in Phase II clinical trial.
- Click the button “Calculate” to obtain
a) value of ni, the number of patients to be recruited in stage i
b) value
of ai, the acceptance points in stage i
c) value of ri, the rejection points in stage i.
Assumption:
1.
Assume
that a Phase I trial of the experimental treatment regimen has been completed,
from which the proper dosages yielding acceptable toxicity have been
established.
2.
Probability
of type I error is smaller or equal than that of type II error (
).
3.
A
maximum of K=1,2 or 3 tests is adopted in the
calculator, since more frequent testing would not seem to be necessary in most
Phase II trials.
4.
Due
to the very limited number of patients who are eligible for a given Phase II
study, and also to the large number of treatment regimens generally awaiting
Phase II trials, the sample size N
for a given trial is frequently fixed in advance.
5.
A
certain number of Phase II trials are terminated due to extreme response
probability results, not due to other causes such as excessive toxicity or
unexpectedly inadequate patient accrual.
Theory:
Typically,
a Phase II trial is designed to have a single stage in which N evaluable patients accrue, are
treated, and are then observed, so that the number, S, who experience a regression is determined. In a multiple testing
procedure patients accrue in several stages, testing being performed at each
stage after appropriate patient accrual has been completed. This feature is
particularly appealing in a clinical setting where there are compelling ethical
reasons to terminate a Phase II trial early if the initial proportion of
patients experiencing a tumor regression is too low or too high.
Specify
largest response probability, p0,
which if true clearly implies the treatment regimen does not warrant further
investigation and smallest response probability, pA, which if true
would implies that the treatment regimen has therapeutic efficacy which
warrants further investigation.
We
have one-sided hypotheses to be tested as 
Suppose
that one decides to perform K stages
and to allow ni
patients to accrue between the (i-1)th and i-th stage, so 
. Let
,
, represent the number of treatment
response among the ni
patients, so 
. Denote the set of acceptance points (of H0) by (
) and the set of rejection points (of H0) by (
). Setting
General
multiple testing procedures (proposed by Schultz et al. (1973)):
At
Stage g (
),
if 
, terminate the trial and reject
;
if 
, terminate the trial and reject
;
if
, continue to Stage g+1.
(Proposed
by O’Brien and Fleming (1979)), at Stage g, would reject H0 whenever
where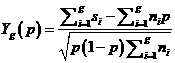
Let 
, where zp denotes the
p-quantile of the standard normal distribution.
Rejection of HA at Stage g < K would occur whenever
.
The
corresponding acceptance and rejection points are specified in the following
manner:
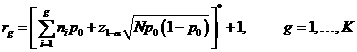
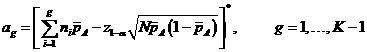
where
denotes the nearest integer to x.
Discussion:
1. Here is some introduction to single-stage procedure so that readers have a clear mind between the difference of single-stage procedure and multiple testing procedures.
The single-stage
procedure can be based upon the statistic
, by rejecting H0 whenever 
is large or 
.
2. Fleming has shown that well-designed group sequential procedures are more efficient than single stage procedures in that they require fewer patients to achieve a predetermined size and power.
3. The multiple testing procedures will require, on the average, fewer patients than the single-stage procedure having similar power. It is more desirable to use a multiple-stage procedure over a single-stage procedure.
4. A choice of either the Stage 1 or Stage K sample size should not be much less than N/K due to the resulting high degree of conservatism which would be required at a very early first test, and, at Stage K , to a resulting apparent small loss in efficiency.
5. To obtain useful and efficient designs, approximately equal sample sizes for each stage is recommended.
Statistical
Notations:
α: The
probability of type I error (significance level) is the probability of rejecting the true null
hypothesis.
β: The
probability of type II error (1 – power of the test) is the probability of
not rejecting the false null hypothesis.
Example:
Since Phase I
studies indicate that the experimental regimen is somewhat more toxic than the
standard, in phase II clinical trial, it is decided to set p0=0.2 and pA=0.4, the maximum 25 patients accrual in 2
stages (Nmax=25, Numstage=2).
A one-sided significance level test (α
=0.05) with 80% power (β=0.2), the number of patients to accrue in stage 1 is 15 (n1=15)
and in the last stage (stage 2), 25 patients are tested (n2=10). The
acceptance points and rejection points in stage 1 is 3 and 7 respectively (a1=3,
r1=7), it means that if the number of treatment response in stage 1
is less than or equal to 3, then stop the study and reject the alternative
hypothesis
, if the number of treatment response in stage 1 is greater
than or equal to 7, then stop the study and reject the null hypothesis
, if the number of treatment response in stage 1 is greater
than 3 and less than 7, then continue to stage 2 to recruit 10 more patients.
The acceptance points and rejection points in stage 2 is 8 and 9 respectively
(a2=8, r2=9), it means that if the number of treatment
response in stage 2 is less than or equal to 8, then stop the study and reject
the alternative hypothesis
, if the number of treatment response in stage 2 is greater
than or equal to 9, then stop the study and reject the null hypothesis
.
Reference: Fleming (1982) Biometrics 38: 143-151