Sample Size Calculator: Two Parallel-Sample Means

Hypothesis: One-Sided Non-Inferiority / Superiority

 

Data Input: (Help) (Example)

Input

 

Results

α

 

 

 

β

 

 

Allowable difference

 

n

Population variance

 

 

 

δ

 

 

 

 

Note:

Variables

Descriptions

α

One-sided significance level

1-β

Power of the test

Allowable difference

Acceptable mean difference between sample two and sample one (µ2-µ1)

Population variance

Population variance

δ

δ>0 for the superiority margin or δ<0 for the non-inferiority margin

n

Sample size of each group

Help Aids Top

 

Application: This procedure is used to test non-inferiority and superiority that can be unified by the following hypotheses:

 

When δ>0, the rejection of the null hypothesis indicates the superiority of the test drug over the control.

When δ<0, the rejection of the null hypothesis indicates the non-inferiority of the test drug against the control.

 

Procedure:

  1. Enter

a)      value of α, the probability of type I error

b)      value of β, the probability of type II error

c)      value of allowable difference

d)     value of Population variance

e)      value of δ>0, the superiority margin or value of δ<0, the non-inferiority margin.

  1. Click the button “Calculate” to obtain result sample size of each group n.

 

Formula:                                                        (*)

 

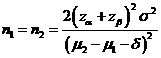Notations:

 

α:           The probability of type I error (significance level) is the probability of rejecting the true null hypothesis.

 

β:           The probability of type II error (1 – power of the test) is the probability of failing to reject the false null hypothesis.

 

δ:           Clinically meaningful difference. The largest change from the reference value (baseline) that is considered to be trivial.

 

μ2 – μ1:  Value of allowable difference is the true mean difference between a test drug (μ2) and a placebo control or active control agent (μ1).

 

Examples

 

Example 1: Consider the difference of 5% is a difference of clinical importance, thus the non-inferiority margin is chosen to be 5% (i.e., δ=-0.05). Also, suppose the true difference in mean of low density lipidproteins (LDLs) between treatment groups is 0% (i.e., μ2(test) – μ1(control)=0). Thus, by using (*), with the standard deviation is 10% (i.e., expected variance is 0.01), the required sample size to achieve an 80% power (β=0.2) at α=0.05 for correctly detecting such difference of 0.5 change obtained by normal approximation as n=50.

 

 

Reference: Chow, Shao and Wang, Sample Size Calculations In Clinical Research, Taylor & Francis, NY. (2003) Pages 57-59.

 

Top