Sample Size Calculator: Two Crossover-Sample Means

Hypothesis: One-Sided Non-Inferiority / Superiority

Data Input: (Help) (Example)

Input			Results
α
β
Allowable difference			n
Population variance
δ

Note:

Variables	Descriptions
α	One-sided significance level
1-β	Power of the test
Allowable difference	Acceptable mean difference between sample two and sample one (µ₂-µ₁)
Population variance	Population variance
δ	δ>0, the superiority margin or δ<0, the non-inferiority margin
n	Sample size of each group

Help Aids Top

Application: This procedure computes sample size for non-inferiority and superiority tests in 2×2 cross-over designs in which the outcome is a continuous normal random variable. A non-inferiority test tests that the treatment mean is not worse than the reference mean by more than a small equivalence margin. The actual direction of the hypothesis depends on the response variable being studied. A superiority test tests that the treatment mean is better than reference mean by more than a small equivalence margin. The actual direction of the hypothesis depends on the response variable being studied. The following hypotheses are usually considered: _.

Procedure:

Enter

a) value of α, the probability of type I error

b) value of β, the probability of type II error

c) value of allowable difference

d) value of population variance

e)      value of δ>0, the superiority margin or value of δ<0, the non-inferiority margin.

Click the button “Calculate” to obtain result sample size of each group n.

Formula:                                                                                                             (*)

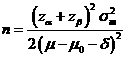Notations:

α:               The probability of type I error (significance level) is the probability of rejecting the true null hypothesis.

β:               The probability of type II error (1 – power of the test) is the probability of failing to reject the false null hypothesis.

δ:               Clinically meaningful difference. The largest change from the reference value (baseline) that is considered to be trivial.

μ₂– μ₁:      The true difference between the two mean values at which the power is calculated.

Population variance:   The within mean square error from the ANOVA table used to analyze the Cross-Over design.

Examples

Example 1: Suppose you want to consider the sample size of a balanced, cross-over design that will be analyzed the t-test approach. Thus when the non-inferiority margin is δ=-0.05, the true difference between the means under H₀ is assumed to be 0, with population variance of 0.01 and the significance level of α=0.05 given. We have the sample size to achieve 80% power for both values of at β=0.2 is n=13.

Reference: Chow, Shao and Wang, Sample Size Calculations In Clinical Research, Taylor & Francis, NY. (2003) Pages 63-68.

Top