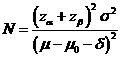Sample Size Calculator: One Sample Mean

Hypothesis: One-Sided Non-Inferiority / Superiority

Data Input: (Help) (Example)

Input

 

Results

α

 

 

 

β

 

 

Allowable difference

 

N

Population variance

 

 

 

δ

 

 

 

 

Note:

Variables

Descriptions

α

One-sided significance level

1-β

Power of the test

Allowable difference

Acceptable difference between sample mean and known or expected population mean (µ-µ0)

Population variance

Population variance

δ

δ>0 for the superiority margin or δ<0 for the non-inferiority margin

N

Sample size

Help Aids Top

 

Application: This procedure is used when the test object (i.e., drug) is concluded to be equivalent to a gold standard on average under an acceptable superiority margin. The following hypotheses are usually considered:.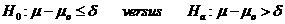

 

When δ>0, the rejection of the null hypothesis indicates superiority over the reference value.

When δ<0, the rejection of the null hypothesis implies non-inferiority against the reference value.

 

Procedure:

  1. Enter

a)      value of α, the probability of type I error

b)      value of β, the probability of type II error

c)      value of allowable difference

d)     value of population variance

e)      value of δ>0, the superiority margin or value of δ<0, the non-inferiority margin.

  1. Click the button “Calculate” to obtain result sample size N.

 

Formula:                                                                                      (*)

 

 

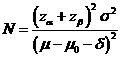Notations:

 

α:               The probability of type I error (significance level) is the probability of rejecting the true null hypothesis.

 

β:               The probability of type II error (1 – power of the test) is the probability of failing to reject the false null hypothesis.

 

δ:               Clinically meaningful difference. The largest change from the reference value (baseline) that is considered to be trivial.

 

μ – μ0:       The value of allowable difference is the difference value between true mean and reference mean (constant value).

 

Examples

 

Example 1: A pharmaceutical company is studying for prevention of progression from osteopenia to osteoporosis they wish to show that the mean bone density post-treatment is no less than pre-treatment by a clinically meaningful (i.e., reduce AMBD) difference δ=-0.5 to test non-inferiority. The difference of mean bone density between before and after treatment is expected to be μ–μ0=0.5. Then the result of sample size at α=0.05 with population variance of 1 for having β=0.2 is N≈7.

 

 

Reference: Chow, Shao and Wang, Sample Size Calculations In Clinical Research, Taylor & Francis, NY. (2003) Pages 50-52.

 

Top